Archimedes Principle
Summary
Archimedes' principle tells us that "any body immersed in a fluid experiences an upward force called thrust, equal to the weight of the fluid displaced by the body".
We apply this principle when we swim, when we throw an object into the water; the object sinks if its weight is greater than the weight of the displaced fluid. The object floats when its weight is less than or equal to the weight of the displaced fluid.
Key words: Principle, Thrust, Fluid, buoyancy, buoyancy, real weight, apparent weight, liquid density, specific gravity, dislodged fluid weight, body density, densimeter.
Abstract
Archimedes's principle indicates us that " any body plunged inside a fluid experiences an ascending force called push, equivalent to the weight of the fluid removed by the body ".
This principle we apply it when we swim, when we throw an object to the water; the object sinks if his weight is greater that the weight of the removed (displaced) fluid.
The object floats when his weight is minor or equal to the weight of the displaced fluid.
Keywords: Principle, Push, Fluid, force of push, flotation, royal weight, apparent weight, density of the liquid, specific weight, weight of the removed fluid, density of the body, densimeter.
Archimedes Principle
"Any body totally or partially immersed in a fluid receives an upward (ascending) thrust equal to the weight of the fluid it dislodges."
A piece of wood floats on water, but a piece of iron sinks. Why does this happen?
Fish move through the water without floating or sinking, perfectly controlling their position. How do they do it?
All the above is related to the upward (ascending) thrust force, which is received by any body immersed in water or any other fluid.
When you lift an object submerged in water, you will have noticed that it is much easier to lift it than when it is not in the water. This is because water and other fluids exert an upward force on any body submerged in the fluid, called buoyancy force or buoyancy force (E), this force is what makes an object appear lighter. This phenomenon is called buoyancy.
The phenomenon of buoyancy is the apparent loss of weight of objects immersed in a liquid. This is due to the fact that when an object is immersed in a liquid, liquids exert pressure on all the walls of the container that contains them, as well as on any body immersed in the liquid. The lateral forces due to hydrostatic pressure acting on the body balance each other, i.e. they have the same value for the same depth. This is not the case for the forces acting on the top and bottom of the body. These two forces are opposite, one due to its weight pushing it downwards and the other, due to the thrust force, pushing it upwards. As the pressure increases with depth, the forces exerted on the lower part of the object are greater than those exerted on the upper part, the resultant of these two forces must be directed upwards. This resultant is what we know as the buoyancy or buoyancy force acting on the body, tending to prevent the object from sinking in the liquid.
When an object is immersed in a liquid, the volume of the immersed body is equal to the volume of fluid displaced. Therefore, the thrust force ρ - V - g, has a magnitude equal to the weight of the fluid displaced by the submerged object.
The thrust that bodies receive when they are introduced into a liquid, was studied by the Greek Archimedes, and its principle is expressed as:
"Any body totally or partially immersed in a fluid (liquid or gas) receives an upward thrust, equal to the weight of the fluid dislodged by the object."
Archimedes' principle is one of the most remarkable discoveries bequeathed to us by the Greeks, and its importance and usefulness are extraordinary. The story goes that King Hieron ordered the making of a crown of pure gold, and to check that he had not been deceived, he asked Archimedes to tell him if the crown had any other metal besides gold, but without destroying the crown. Archimedes was the first to study the vertical upward thrust exerted by fluids.
It is important to note that the thrust force does not depend on the weight of the submerged object, but only on the weight of the displaced fluid, i.e., if we have different materials (steel, aluminum, bronze), all of equal volume, they all experience the same thrust force.
If a sealed one-liter container is half submerged in water, it will displace half a liter of water and the buoyant force (or buoyancy) will equal the weight of half a liter of water, no matter what the container contains. If the vessel is completely submerged, the buoyant force will be equal to the weight of one liter of water at any depth, as long as the vessel is not compressed. This is because at any depth the vessel cannot displace a volume of water greater than its own volume.
To know the magnitude of the buoyancy force we must understand the expression "the volume of water displaced". If we completely submerge an object in a container filled to the brim with water, some water will spill out, and we say that the water is displaced by the object. The volume of the object is equal to the volume of the displaced (spilled) water.
Since the density of water is 1 g/cm3 (1000 kg/m3), the number of grams of mass of water corresponds to the number of cubic centimeters of volume of the object. This is a good method for determining the volume of irregularly shaped objects. A completely submerged object always displaces a volume of liquid equal to its own volume. That is, the volume of the body is equal to the volume of liquid displaced.
Whether an object floats or sinks in a liquid depends on how the buoyancy force compares to the weight of the object. The weight in turn depends on the density of the object.
According to the magnitude of these two forces we have the following cases:
1) If the weight of the submerged object is greater than the thrust force, the object will sink.
2) If the weight of the body is equal to the thrust force it receives, the object will remain floating in equilibrium (part inside the liquid and part outside it).
3) If the weight of the submerged object is less than the thrust force it receives, the object will float on the surface of the liquid.
Archimedes' principle applies to objects of any density. If the density of the object is known, its behavior when immersed in a fluid can be:
1) If the object is denser than the fluid in which it is immersed, the object will sink.
2) If the density of the object is equal to the density of the fluid in which it is immersed, the object will not sink or float.
3) If the object is less dense than the fluid in which it is immersed, the object will float on the surface of the fluid.
Due to the effect of buoyancy, bodies immersed in a fluid have a weight apparently less than their true weight, and we call it apparent weight. The value of the buoyancy force is determined by the difference of the real weight and the apparent weight, i.e:
Thrust = actual weight - apparent weight
Since any body that is immersed in a liquid will adjust to a depth at which its weight is equal to that of the displaced water, the weight of the body is given by the expression:
Fcpo = Pcpo = ρcpo - Vcpo - g
and the weight of the displaced fluid or buoyancy force exerted by the liquid is given by the expression:
E = ρliq - Vcpo - g
where:
E = is the thrust
Vcpo = the volume displaced by the body
ρliq = the density of the liquid in which the body is immersed
g = 9.81 m/s2
As the specific gravity (Pe) of the substance is given by:
Pe = ρliq - g
Then we can also write the expression:
E = Pe - Vcpo
The product of the volume of the body by the density of the fluid is equal to the mass of the dislodged fluid, corresponding to a volume identical to that of the submerged body. The product of this mass by the acceleration of gravity gives its weight. Therefore. We can also calculate the thrust suffered by bodies immersed in a fluid using the expression:
E = Vcpo - ρliq-g=mlíq - g
According to the above, the thrust received by a body immersed in a liquid can be determined by one of the following expressions:
Thrust = Weight of displaced fluid
Thrust = Real weight - apparent weight in the liquid
Thrust = (density of the body) (volume of the submerged body) (gravity)
E = ρcpo - Vcpo - g
Thrust = (Specific gravity of substance) (Volume of liquid dislodged)
E = Pe - Vcpo
Thrust = (mass of displaced liquid) (gravity)
E =mlíq - g
Thrust = (density of liquid) (volume of liquid dislodged) (gravity)
E = ρliq - Vliq - g
It should be remembered that for the application of the above formulas, in case the body is totally submerged, the volume of the body is equal to the volume of liquid dislodged, and that when the body floats partially in the liquid, the volume of liquid dislodged is equal only to the volume of the part of the body that is submerged.
The concept of buoyancy can help us to determine the density of a solid body (ρcpo). To do this we first determine the actual mass mr of the body with the help of a balance. Then we immerse the object in a liquid of known density (ρliq.c), e.g., water and determine the apparent mass of the object ma, , which will be less than the previous one. According to Archimedes' principle, this difference is due to the buoyancy of the water, and therefore the difference mr -ma is equal to the mass of the water dislodged by the body. The density of the body is given by the expression:
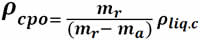
We can also determine the density of a liquid. To do this, we first obtain the apparent mass ma of a body of mass mr immersed in a liquid of known density(ρliq.c). The difference in mass (mr -ma) is equal to the mass of the volume of liquid dislodged, thus:
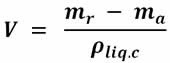
Then the same body is introduced into the problem liquid and we find its apparent mass ma2. Again the difference in mass mr -ma2 is equal to the mass of the dislodged liquid volume, therefore:
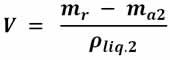
Since the volume must be equal in both equations, since the body is the same, we have that the density of the (unknown) problem liquid is:
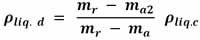
Some of the applications of Archimedes' principle are: buoyancy of ships, buoyancy of submarines, life jackets, hydrometers, hot air balloons, toilet box floats, fish.
Boats float because their submerged part displaces a volume of water whose weight is greater than the weight of the boat. The materials from which a boat is built are denser than water. But because the boat is hollow inside, it contains a large amount of air. Because of this, the average density of the boat is less than that of water.
Because, for an object to float, the buoyant force on the body must be equal to the weight of the displaced fluid, denser fluids exert a greater buoyant force than less dense fluids. Therefore, a boat floats higher in salt water than in fresh water because the former is slightly less dense.
A submarine normally floats. It is easier for a submarine to vary its weight than its volume to achieve the desired density. To do this, water is let in or out of the ballast tanks. Similarly, a crocodile increases its average density when it swallows stones. Because of its increased density (due to swallowed stones), the crocodile can dive deeper underwater and is less exposed to its prey.
In order for a person to float in the water more easily, his density must be reduced. To do this, the person puts on a life jacket, causing his volume to increase while his weight increases very little, so his density is reduced.
A fish normally has the same density as water and can regulate it by extending or compressing the volume of a bag it has. Fish can move up by increasing their volume (which decreases their density) and move down by decreasing their volume (which increases their density).
The densimeter or hydrometer consists of a glass tube with a tube filled with lead so that it floats vertically. The upper part has a graduation that directly indicates the density of the liquid in which it is placed. It is used to measure the amount of alcohol in a wine, to control the purity of milk, to know if an accumulator is charged (the charge depends on the acid concentration of the liquid in the accumulator).
TABLE 1 DENSITY OF DIFFERENT SUBSTANCES
| Substance | Density (kg/m3) | Substance | Density (kg/m3) |
| Water at 4 ºC | 1000 | Gasoline (20 ºC) | 700 |
| Water (20 ºC) | 998 | Glycerin at 0ºC | 1250 |
| Seawater | 1030 | Ice | 920 |
| Air (0 ºC) | 1.30 | Helio | 0.18 |
| Air (20 ºC) | 1.20 | Mercury(0 ºC) | 13600 |
| Ethyl alcohol | 790 | Oxygen | 1.43 |
| Aluminum at 0ºC | 2700 | Gold at 0ºC | 19300 |
| Copper at 0ºC | 8900 | Silver at 0ºC | 10500 |
| Cork at 0ºC | 240 | Lead | 11400 |
We will now carry out the solution of some problems by applying the Archimedean principle.
Example 1
A sphere of a certain material is immersed in water, its apparent mass turned out to be 91.3 g. Its real mass (in air) is 100 g.
a) What is the density of this sphere?
b) We then submerge the same sphere in another liquid of unknown density ρliq.d, and the apparent mass of the sphere is found to be 93.04 g. What is the density of this liquid?
Data:
mr = 100 g = 0.100 kg
ma = 91.3 g = 0.0913 kg
ρwater = 1000 kg/m3
ρliq.d = 1000 kg/m3
a )Formula:
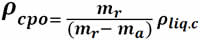
Substitution and result:

According to the density table, we deduce that the sphere is made of lead, whose density is 11400 kg/m3.
b) Data:
mr = 100 g = 0.100 kg
ma = 91.3 g = 0.0913 kg
ρwater = 1000 kg/m3
ma2 = 93.04 g = 0.09304 kg
Formula:
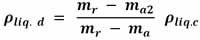
Substitution:

Example 2
A wooden cube has a mass of 10 kg and measures 30 cm on each side, it is kept submerged under water.
a) What is the thrust on the wooden bucket?
b) What force is needed to keep the bucket submerged?
Data:
m = 10 kg
Edge = 30 cm.
Density of water = 1000 kg/m3
Formulas:
V = l - l - l
E = ρ - V - g
Substitution:
a) V = (0.30 m)(0.30 m)(0.30 m) = 0.027m3
E = (1000 kg/m3) (0.027 m3) (9.81 m/s2) = 264.87 N
b) To keep the block submerged, the thrust force must be balanced with the force to keep the cube submerged plus the weight of the cube, according to the above: E = F + mg, therefore, the force required to keep the cube submerged is:
F = E - m - g = (264.87 N) - (10 kg) (9.81 m/s2) = 255.06 N
Example 3
The cube of a certain material measures 20 cm on each side, has a mass of 7.2 kg.
a) Will it float in the water?
b) And if it floats, what is the height of the cube that rises above the surface of the water?
Solution:
a) The volume of the cube is V = (0.20m) (0.20m)(0.20m)= 0.008 m3, so its density is: ρ = m/V = (7.2 kg) / 0.008 m3 = 900 kg/m3
Since the density of water is 1000 kg/m3, then the density of the water is greater than that of the cube, so the cube will float.
b) remembering that any body that is immersed in a liquid will adjust to a depth at which its weight is equal to that of the displaced water, as the weight of the object is given by the expression:
Fcpo = Pcpo = ρcpo - Vcpo - g
and the weight of the displaced fluid or buoyancy force is:
Eqpo = ρliq - Vliq - g
Equating both expressions we have that:
ρcpo - Vcpo - g = ρliq - Vliq - g
whereby:

Therefore: Vliq = (0.90) Vcpo, so the volume of the displaced liquid is 0.90 of the volume of the cube, that is, 90% of the cube is submerged. This means that 10% of the volume of the cube is out of the water, that is:
Vsobresale = (0.10) Vcpo = (0.10) (0.008 m3) = 0.0008 m3
The area of each side of the cube has a value of: (0.20 m) (0.20 m) = 0.04 m3 therefore, the overhang (h) of the cube is:
h = (Vsobresale) / A = (0.0008m3) / (0.04m2) = 0.02 m = 2 cm.
Example 4
A queen's crown has a mass of 1.30 kg. But when the mass is determined while fully immersed in water, its apparent mass is 1.14 kg. Is the crown solid gold?
Solution:
The data we are given are: the real mass and the apparent mass of the object, we know the density of the "supposed" material of the crown, which is 19300 kg/m3, plus the density of the fluid "water" (1000 kg/m3). Therefore to give the answer, we must prove that the density of the body is or is not 19300 kg/m3.
Using the formula:
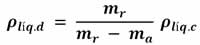
to determine the density of the body, and substituting the values of real mass, apparent mass and density of water, in the above formula we have that the density of the body is:
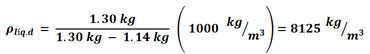
With the result that the density of the body is 8125 kg/m3 according to the mass values obtained, we observe that it does not coincide with the density of gold (19300 kg/m3); therefore we conclude that the crown is not solid gold.
Bibliographic reference
Pérez Montiel, Héctor (2011) FISICA GENERAL BACHILLERATO, Grupo Editorial Patria, edition 4.
Hewitt, Paul G., (2009), Concepts of Physics, Editorial Limusa S.A. de C.V.
Tippens, Paul E. (2011), Physics concepts and applications, Publisher: MCGRAW HILL, edition 7.
[a] Teacher at Escuela Preparatoria No. 4